How to Write in Binary Code?

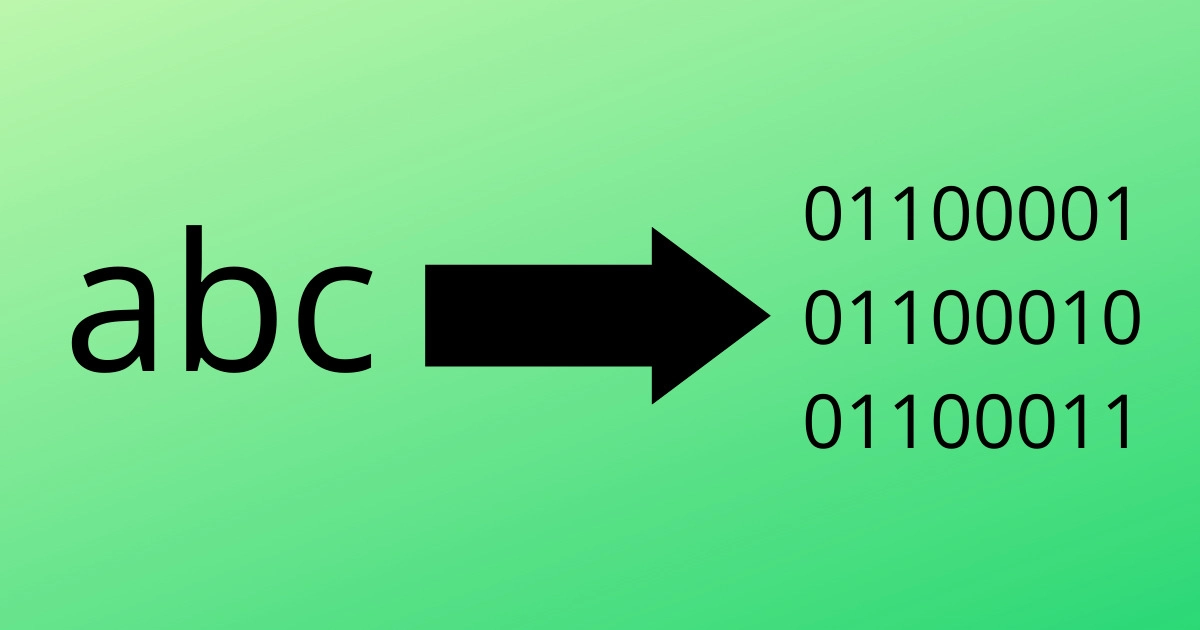
Due to the fact that computers are unable to understand programming languages, it is necessary to convert the programming codes into machine-readable code. As we all know, binary code is a high-level language and can’t understand by a human. For those who want to learn or understand binary languages, there are many ways, like using the online Binary Code translator to convert the code manually.

Moreover, to understand the binary code, you have complete knowledge of what exactly binary is. In digital computers, binary code is based on a binary number system in which only two states are off and on, usually depicted by a 0 or 1. 

Binary systems represent each digit position as a power of 2 (4, 8, 16, Etc.) in contrast to decimal systems, which employ ten digits (10, 100, 1,000, Etc.). In simple words, binary codes are electrical signals that represent numbers, characters, and operations.

The information provided here is sufficient for understanding the basic concept of binary code. So, let’s understand how to write binary code.

Steps to Write Binary Code

As we all know, binary language is not a simple language; there are many complexities in understanding binary coded languages because of their complex syntax structure. The best way to understand the binary syntax in a short time, you need to you online Binary Code to Text tools.

In order to understand the syntax of binary language, you simply need to follow the following steps:

Manual Method

In order to understand how to convert binary code to text in-depth, you need to follow the following steps:

Use ASCII to Write Binary Code

If you work in the technical field, you must know about the ASCII code for characters on these computers. Moreover, if you had experience in programming office, the interviewers probably asked about this system. 

It is the most common method of converting code to letters. In computer systems, one hundred twenty-eight characters are interpreted as numbers that allow data to be transferred between systems representing these characters. 

It is important to note that the UTF-8 binary code matches this code for lettering. In the same way, the binary code is different from lowercase letters.

ASCII code introduced its own table in which binary codes are stored. To understand the ASCII code, you need to learn the table of ASCII.

Example:

ASCII String:

“Help”

Convert into sting:

01101000 01100101 01101100 01110000 

Calculate Code to Find Out the Letter it Corresponds to

In binary coding, zeros and ones act as on-and-off switches. When you see zeros, the value is referred to as “off,” which means the zero is not factored into the calculation. The one is “on” and is used to determine which number corresponds to the binary code.

Example

Using the binary code 01001111, all you are doing is calculating the ones. The numbers should be squared from right to left using the digit 2^n. Let us begin by calculating the correspondence between the numbers and the value:

Using the binary code 01001111, all you are doing is calculating the ones. The numbers should be squared from right to left using the digit 2^n. Let us begin by calculating the correspondence between the numbers and the value:

1 = 2^0

1= 2^1

1 = 2^2

1 = 2^3

0 = 2^4

0 = 2^5

1 = 2^6

0 = 2^7

The calculation is as follows:

1 = (1 x 2^0) = 1

1= (1 x 2^1) = 2

1 = (1 x 2^2) = 4

1 = (1 x 2^3) = 8

0 = Because zeros are off, calculations will always equal 0.

0 = zero here too

1 = (1 x 2^6) = 64

0 = 0

It would be 79 if 64, 8, 4, 2, and 1 were added together. According to the ASCII chart, that corresponds to the letter O.

Use the Code to Formulate Words

Using these codes, you can create words by combining letters. In simple terms, these words indicate what functions the computer must perform for the user to use it.

Example:

It is known that the code for the letter O is 01001111, so we were looking for the word OK. Check the ASCII chart to see if code 01001011 corresponds to the letter K. Based on the ASCII chart; the total calculation is 75. Here is a quick look at it.

1 = 2^0

1 = 2^1

0 = 2^2

1= 2^3

0 =2^4

0 =2^5

1 = 2^6

0 = 2^7

The final calculation is as follows:

1 = (1 x 2^0) = 1

1 = ( 1 x 2^1) = 2

0 = 0

1= (1 x 2^3) = 8

0 = 0

0 = 0

1 = (1 X 2^6) = 64

0 = 0

64 + 8 + 2 + 1 = 75 = K

Calculation of binary values: 01001111 + 01001011 = OK

Online Method

Many users don’t want to waste their time doing manual calculations. Those who want a quick solution need to use online Binary Code for Text tools. By using those tools, the user only needs to enter the string the tool will automatically convert the strings into binary code.

Bottom Line:

As we discuss above, you can easily convert binary code to text or vice verse manually or by using online Binary Code to Text converter tool.